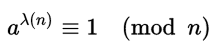每天学点数学
数学中的一些美丽定理具有这样的特性：它们极易从事实中归纳出来，但证明却隐藏的极深。– 高斯 在数学你不明白任何东西。你只使用它们。– 冯·诺伊曼
哥德巴赫猜想
概念
任一大于2的偶数，都可表示成两个素数之和。 而将一个给定的偶数分拆成两个素数之和，则被称之为此数的哥德巴赫分拆。 换句话说，哥德巴赫猜想主张每个大于等于4的偶数都是哥德巴赫数——可表示成两个素数之和的数。
欧拉注明此一猜想可以有另一个等价的版本:
1(A): 任一大于2的偶数都可写成两个质数之和。
2
3(B): 任一大于5的奇数都可写成三个素数之和。
今日常见的猜想陈述为欧拉的版本，(A)亦称为“强哥德巴赫猜想”或“关于偶数的哥德巴赫猜想”。(B)称为“弱哥德巴赫猜想”或“关于奇数的哥德巴赫猜想”。其中(B)从(A)推出，所以如果(A)得证那么(B)也得证。
证明
陈氏定理（陈景润的）
所谓“陈氏定理”的“1+2”，是指：对于任给一个大偶数 N，总可以找到奇素数p', p'‘或p1,p2,p3，使得下列两式至少有一个成立：
1N = p' + p''
2N = p1 + p2p3
两式可以同时成立。偶数较小时，如 N=62，则可以有 62=43+19 以及 62=7+5×11
欧拉定理
概念
定理一 连通的无向图有欧拉路径的充要条件是：
G中奇顶点（连接的边数量为奇数的顶点）的数目等于0或者2。
连通的无向图是欧拉环（存在欧拉回路）的充要条件是：
G中每个顶点的度都是偶数。
定理二
如果连通无向图G 有 2k 个奇顶点，那么它可以用 k 笔画成，并且至少要用 k 笔画成。
对有向图来说，一笔画不仅指遍历所有边，而且要遵循正确的方向。 严谨地说，一个连通有向图G有欧拉路径，指存在一个顶点，从它出发，沿着有向边的方向，可以不重复地遍历图中所有的边。 有向图的欧拉回路则是指可以从某一顶点开始，沿有向边的方向不重复地遍历所有边，然后回到原来出发的顶点。用类似于定理一中证明的思路，可以得到有向图一笔画的判定准则：
一个连通的有向图可以表示为一条从顶点u到v的（不闭合的）欧拉路径的充要条件是：
u的出度（从这个顶点发出的有向边的数量）比入度（指向这个顶点的有向边的数量）多1， v 的出度比入度少1，而其它顶点的出度和入度都相等。
一个连通的有向图是欧拉环（存在欧拉回路）的充要条件是以下两个之一：
1 1.每个顶点的出度和入度都相等；
2 2.存在一系列的（有向）环C1 C2... Cm，使得图G里的每一条边都恰好属于某一个环。
一笔画问题讨论的是能否不重复地遍历一个图的所有边，至于其中有否顶点的遍历或重复经过则没有要求。哈密顿问题讨论的则是顶点的遍历：能否不重复地遍历一个图的所有顶点？
参考： Tutorials How to find whether a given graph is Eulerian or not? Sketch of Eulerian Circuit Algorithm
同余定理
数学上，同余（英语：congruence modulo，符号：≡）是数论中的一种等价关系。当两个整数除以同一个正整数，若得相同余数，则二整数同余。同余是抽象代数中的同余关系的原型。最先引用同余的概念与“≡”符号者为德国数学家高斯。
定义：两个正整数a,b如果它们初一正整数m所得的余数相同，则称a,b对于模m同余。记作：a≡b(mod m)
性质
性质1：a≡b(mod m) => c*m=a-b ,c属于Z（即是说 a 和 b 之差是 m 的倍数） 换句话说：a≡b(mod m) => m | (a-b) （即是说 m 能整除 a 和 b 之差，同时**m | (a-b) ** 也是a,b关于m同余的充要条件）
性质2： 同余关系具有反身性、对称性与传递性，即
1）a≡a (mod m);
2）若a≡b (mod m), 则b≡a (mod m);
3）若a≡b (mod m), b≡c (mod m)，则a≡c (mod m).
性质3 ：若a≡b(mod m), c≡d (mod m),则
1）a+c≡b+d (mod m);
2）a-c≡b-d (mod m);
3）ac≡bd (mod m).
推论 若a≡b(mod m),n为自然数，则an≡bn (mod m)。
性质4 除法定理一：如果ka≡kb(mod m)，且(m,k)=1（即k和m互质），则a≡b(mod m)
性质4 除法定理二：
也即是说：m 的因数也可以整除(a-b)。
m是n的倍数: m = c *n , n | m , 因为m|(a-b) , 所以 n | (a-b) => a≡b (mod n)
同余关系式
威尔逊定理
威尔逊定理给出了判定一个自然数是否为素数的充分必要条件。 即：当且仅当p为素数时：(p-1)! ≡ -1 (mod p) 但是由于阶乘是呈爆炸增长的，其结论作为了解。
费马小定理
假如a是一个整数，p是一个质数，那么 是p的倍数，可以表示为a^p≡a (mod p)
当(a,p)=1 (a不是p的倍数)时定理可以写为：a^(p-1) ≡1 (mod p)
费马小定理是欧拉定理的一个特殊情况，看下面
欧拉定理
欧拉定理（也称费马-欧拉定理或欧拉函数定理）是一个关于同余的性质:若 n,a为正整数，且 n,a互素（即 gcd(a,n)=1）则
a^φ(n) ≡1 (mod m)
即 a^φ(n)与1在模n下同余；φ(n)为欧拉函数。
当n是素数的时候， φ(n)=n-1，所以欧拉定理变为： a^(n-1) ≡ 1 (mod m) or a^n ≡ a (mod m) 这就是费马小定理。
必须掌握-微积分基础
导数
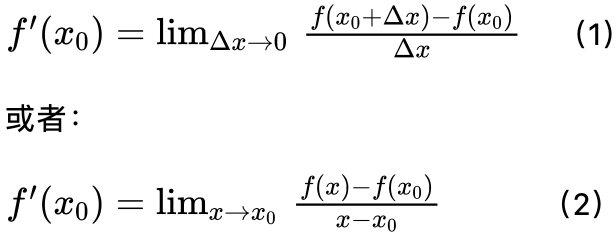
四则运算
